蒙地卡羅模擬不是預測未來，是量化風險分布。

與其期待精準預測，不如學會如何與不確定共處。

0. 什麼是 Monte Carlo 模擬？

Monte Carlo 模擬（Monte Carlo Simulation）其實是一種利用隨機抽樣（random sampling）與統計重複試驗來預測系統結果的數學方法。

它的名字來自於摩納哥的蒙地卡羅（Monte Carlo）賭場(沒錯，就是那個豪華的賭場）——那是代表「機率」與「隨機性」的象徵。

在1940 年代，Stanislaw Ulam 與 John von Neumann 在開發核彈的曼哈頓計畫中，使用這種方法估算中子在物質中的擴散機率。由於該方法需要大量隨機數與運算，他們幽默地取名為 “Monte Carlo”，彷彿就像是賭客在賭場中投出無數次骰子。

Monte Carlo 模擬的核心精神是：

當理論解析困難、歷史樣本不足時，就讓電腦「玩出一千次未來甚至是一萬次未來可能的結果」。所以，它並不是不預測單一結果，而藉由數學方法是創造出可能未來的分布（distribution of outcomes）。

1. Monte Carlo 模擬的科學與金融應用

Monte Carlo 模擬的強大之處在於，它能在「理論模型無法精確推導」的情況下，仍透過大量 #隨機試驗來逼近真實世界的不確定性。也因此，它被廣泛應用於各種領域，從自然科學到行為金融，皆有其身影。

在物理與工程學中，Monte Carlo 模擬被用來模擬光線路徑、粒子運動、以及複雜的流體動態。舉例來說，現代的電腦動畫與光影渲染技術（如 Pixar、NVIDIA RTX 光線追蹤）都依賴 Monte Carlo 方法計算光的隨機反射，呈現逼真的畫面。

在醫學與流行病學領域，它被用於預測疾病傳播、藥物實驗的統計結果與臨床試驗的成功率。研究人員可以根據不同條件（如人口密度、感染率、藥效）進行上千次模擬，推估可能的疫情發展情境。

而在我所處的金融學領域中，Monte Carlo 模擬更是不可或缺的工具。它被大量用來：

• 評估投資組合的風險（例如 Value-at-Risk, VaR，我碩班的論文，血淚史）；

• 進行衍生性商品定價（如選擇權、保險商品）；

• 模擬退休金或財務規劃的「成功機率」。

相比傳統的平均報酬或單一路徑分析，Monte Carlo 模擬能幫助我們看到「未來結果的機率分布」，讓投資人不只關心報酬的高低，也能評估各種極端情境下的結果。

換句話說，這種方法不只是預測「報酬會多少」，而是描繪「報酬可能會在哪裡」。
它讓金融世界從單一的「確定報酬率」，走向「機率化思維」的時代。

2. 為什麼歷史回測（Backtesting）可能會誤導？

我這陣子在FB的貼文受到一些質疑：只截取某段大多頭的時間框架來回測。因此，有人建議我要用Rolling Window Return，甚至建議我要從2000年回測才準確得多。也有人會想：「我用過去 20 年的 S&P 500 回測，平均年化報酬 8%，所以未來也差不多。」
但這樣的想法，其實存在了三個陷阱：

1. 歷史只有一條樣本路徑。
   市場報酬的順序（sequence of returns）對最終結果影響極大。不同的漲跌順序，可能造成完全不同的終值。

2. 市場結構會變。
   通膨、利率、科技周期與地緣政治，都會改變報酬分布。

3. 人類偏誤干擾。
   投資者往往過度信任「平均報酬」，忽略尾端風險（fat-tail risk）。

Monte Carlo 模擬的價值在於，它不預測「確定的未來」，而是讓你看見一千種未來甚至一萬種的可能樣貌。

3. Monte Carlo 的限制：若底層假設錯了，一切都錯

雖然 Monte Carlo 看似科學，但它是假設驅動（assumption-driven）的。結果的準確度取決於你輸入的「報酬分布假設」：

• 若假設報酬為常態分布（Normal Distribution），但真實市場有所謂的厚尾（Fat Tails），那麼會#嚴重低估 極端風險。

• 若假設報酬平均值固定，卻忽略通膨與結構性變化（Non-Stationarity），預測將失真。

因此 Monte Carlo 並非「預言」，而是一面鏡子。它讓我們試著問自己：

若一切只是機率分布——我能承受多大的「風險區間」？

🔍 延伸思考：
Taleb《黑天鵝Black Swan》一書中對「模型錯覺（model error）」的批判。

4. DCA（定期定額）與 Lump-Sum（一次投入）的模擬比較

1️⃣ 模擬設計

• 假設年報酬平均 7%、標準差 15%。

• 比較：

  • DCA：每月固定投入；

  • Lump-Sum：一次投入全部本金。

• 進行 1000 次模擬，觀察終值分布。

2️⃣ 常見結論

• Lump-Sum 平均報酬較高（市場長期上漲，也就是市場常處於多頭）。

• DCA 波動較低，在高估值或不確定期更穩定。

• 機率分布顯示，DCA 的下檔風險控制優於 Lump-Sum，但上檔潛力略低。

3️⃣ 模擬陷阱

• 假設報酬為常態分布 → 低估暴跌期的 DCA 防禦力。

• 忽略通膨、稅務、費用 → 結果過於理想。

• 槓桿 ETF（如 TQQQ） → 應採用 log-normal 或 fat-tail 模型，否則誤導嚴重。

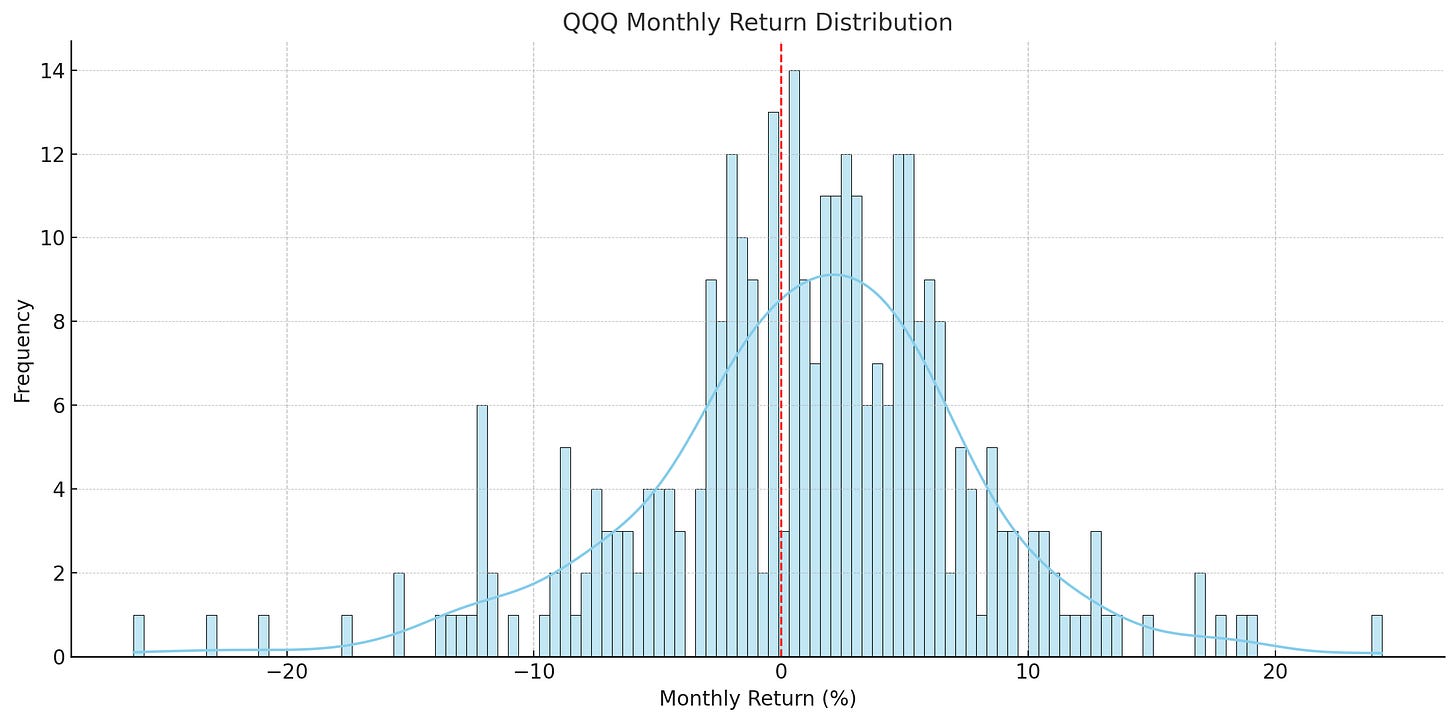
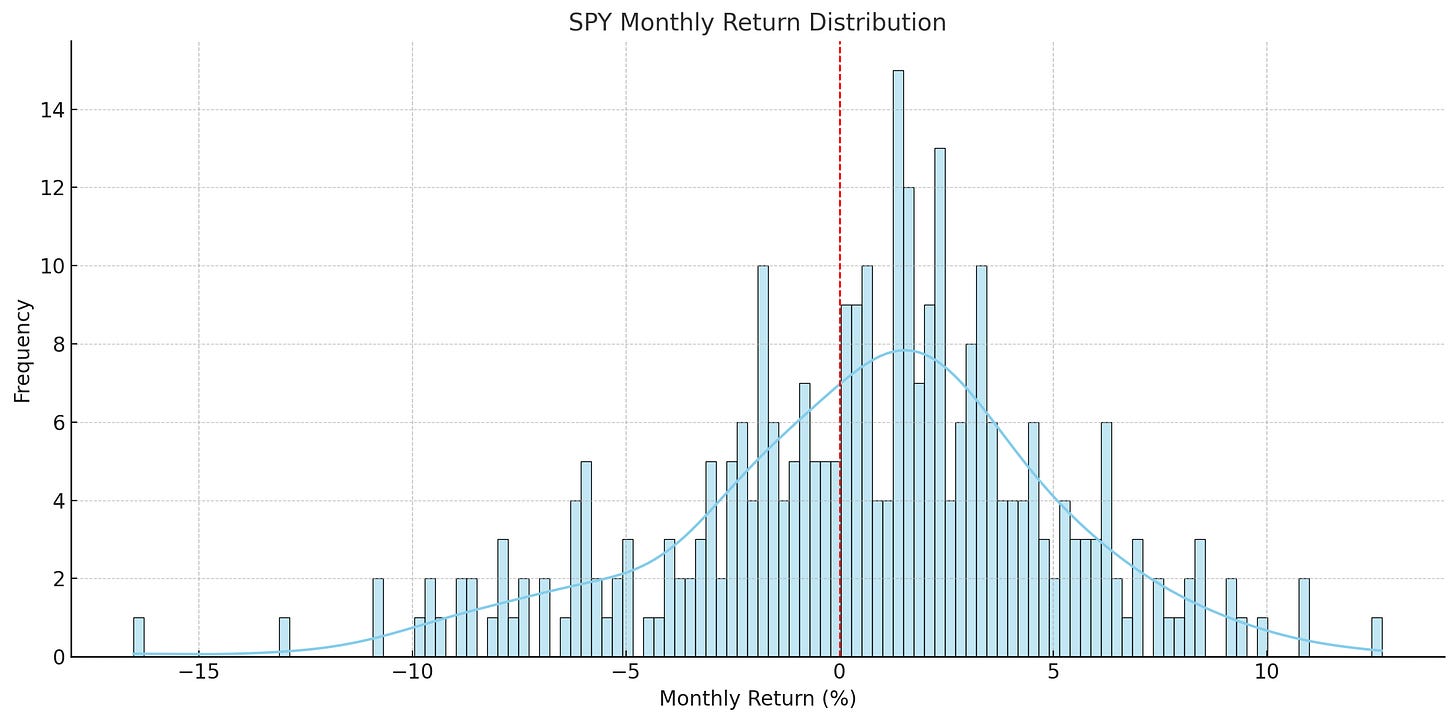
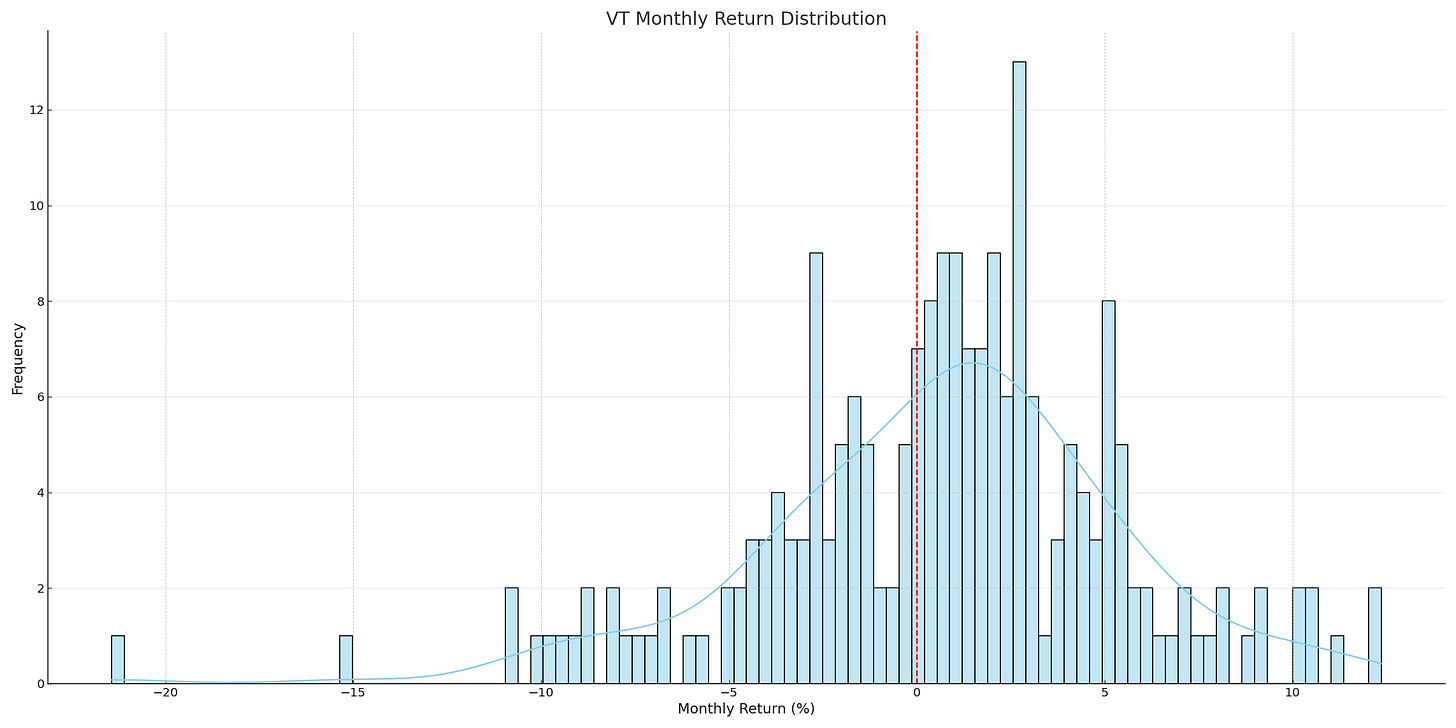
補充觀察：不同資產的月報酬分布圖

從 SPY、QQQ、VT、TQQQ 的歷史月報酬分布圖中，我們可以清楚看出幾個關鍵差異：

• SPY、QQQ：分布大致接近常態，左尾略長，且平均月報酬介於 +0.5%～+1.0%。大盤ETF的波動與下行風險相對可控。

• VT：報酬分布偏右，全球配置的特性使其月報酬較集中在 0%～5%，極端正負報酬機率略低。

• TQQQ：呈現高度尖峯厚尾（fat-tail）特徵，單月跌幅超過 -30%、漲幅超過 +40% 都有出現，明顯違反常態分布假設。

這些差異說明，若模擬時仍假設報酬服從常態分布，將大幅低估像 TQQQ 這類槓桿資產的#極端風險與 DCA 在暴跌期的潛在防禦優勢。

5. 如何正確解讀 Monte Carlo 結果

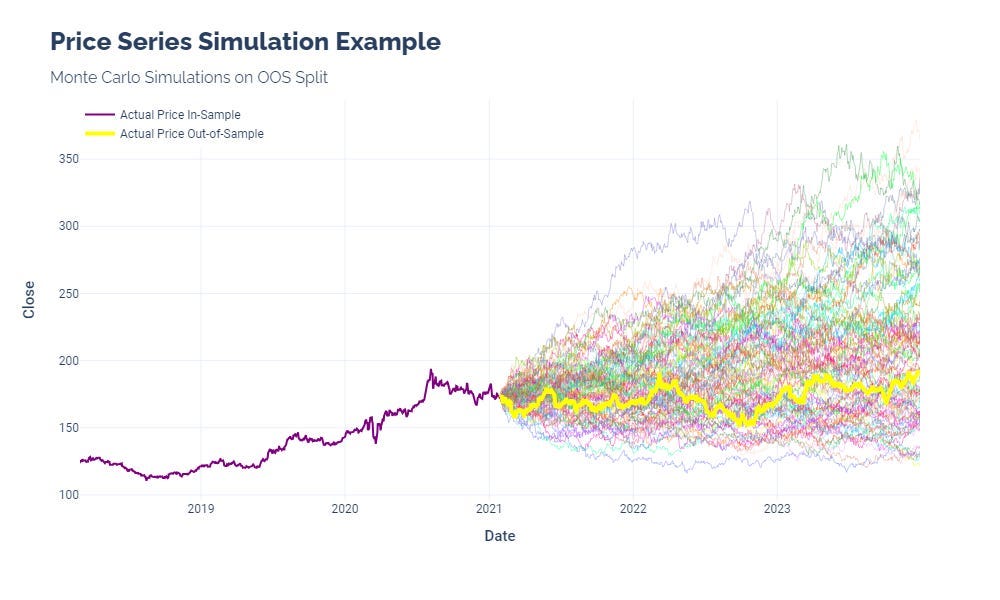
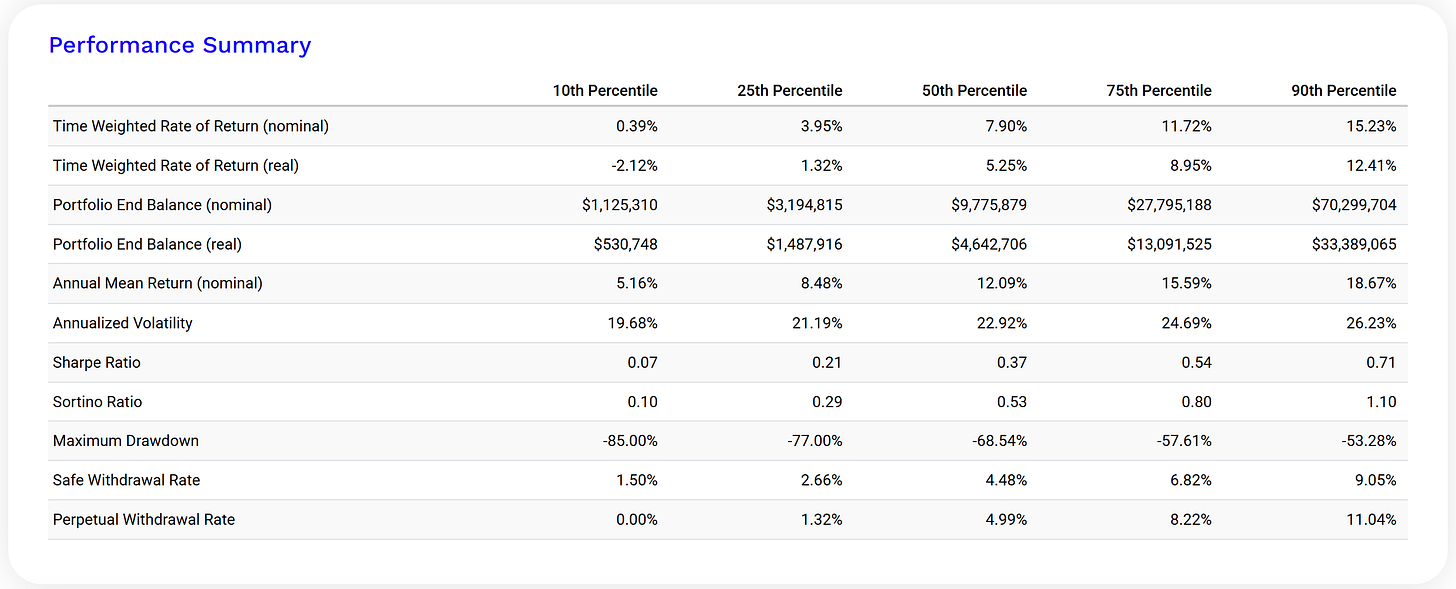
下圖為利用Portfolio Visualizer 模擬QQQ ETF以一百萬本金進場，三十年後的機率分佈狀況。點此連結: Portfolio Visualizer

5.1 為什麼模擬結果中的「機率」這麼重要？

▪ 模擬其實不是預測的水晶種，而是在幫你「看一千種未來」

很多人一看到模擬報表裡有「$9,777,000」或「年化 14.7%」，就誤以為那是「大多數人會拿到的結果」。事實上，Monte Carlo 模擬不是預測你會賺多少，而是在電腦裡跑出一千條不同甚至更多的未來路徑，然後告訴你：這些路徑裡有幾條讓你過得舒服、有幾條讓你資金見底。

▪ 所謂「中位數」，只是 50% 成功的分界點

如果模擬結果顯示你的中位數終值是 900 萬，那代表有一半的情境你其實拿不到這麼多。也就是說，這不是「最可能」的結果，而是剛好一半高於它、一半低於它。真正重要的，是那低於它的那一半裡，最差會差到什麼程度？

▪ QQQ 的風險，在於「好情境很好，壞情境很慘」

QQQ 的模擬結果中，10% 壞情境可能只剩 50 萬，90% 好情境則可能超過 7000 萬。這個差距代表的不是報酬好壞，而是風險結構的極端不對稱。如果你剛好不幸落在那個「最差 10%」的機率裡，過去模擬出來的高報酬對你沒有任何幫助。

▪ 成功率的高低，反映你的計畫在多少情境下能撐下去

所謂「70% 成功率」的意思是：模擬裡有 70% 的路徑，你的資產夠你活到最後，不會破產。反過來說，還有 30% 的路徑你會提領過快、資產提早見底。你願意冒這 30% 的風險嗎？這不是數學方法能告訴我們的，而是我們對未來不確定性的容忍度所決定的。

---

5.2 Monte Carlo 模擬的真正價值，是在於它能讓你看見目標達成的機率範圍。

當我們模擬一個投資計畫時，不論是存房屋首購或退休基金，結果通常會以「成功率」呈現。例如：

模擬結果顯示有 70% 的機率能達成退休金目標。

也就是Monte Carlo模擬的真義是：

1️⃣ 不是要找「最可能」，而是要理解「可能的範圍」

許多人在看 Monte Carlo 結果時，仍會下意識地找「平均值」或「中位數」。但投資報酬不是體重或身高，＃平均值的意義極其有限。
真正值得關注的，是整個分布的「形狀」與「尾端風險」——也就是在最壞情境下，你的資產是否仍能支撐我們的財務目標？

例如，兩個投資方案的中位報酬率可能相同，但若其中一個在最壞 10% 的情境下會讓你提前破產，那它實際的風險就高得多。Monte Carlo 模擬讓這種差異一目了然。

---

2️⃣ 從「數字」回到「人」

每一條模擬曲線背後，其實都是一種人生劇本。有些人在模擬中「早早達標」，象徵他們可能在順風市場中提前財務自由；也有些人在模擬後期「資金見底」，再再都提醒我們通膨、醫療費或長壽風險都可能侵蝕資產。

因此，Monte Carlo 模擬最終不單單是一場關於數學方法的遊戲，而是一種關於選擇與價值觀的對話。它讓我們學會問自己：

• 我是否能接受某種機率下的失敗？

• 如果真的失敗，我是否有備案、有彈性？

• 我投資的目標是「最大化報酬」，還是「最小化後悔」？

---

3️⃣ 機率思維：理財的成熟標誌

當我們開始解讀 Monte Carlo 模擬，代表開始用機率思維而非「命中註定」的方式理解市場。我們會明白金融投資沒有「保證」，只有「機率分布」；也當我們開始以這樣的方式思考，不僅能做出更穩健的投資決策，也能在生活中培養出更寬廣的視野——因為你不再追求完美的答案，而是學會在不確定（風險）中找到平衡。

6. 機率思維，才是真正的風險管理

我們經常在談論風險管理時，預設的是「避開壞事發生」。但在退休理財這個主題裡，真正成熟的風險管理，不是避免損失，而是設計出一個「在多數可能情境下都能存活的提領策略」。

歷史不會一再重演，但機率的分布可能會在人的行為與市場動態中持續出現。這正是我們使用蒙地卡羅模擬（Monte Carlo Simulation）的原因：不是為了預測未來的絕對報酬，而是了解不同策略下的「可能會發生什麼」，進而做出風險容忍度相符的設計。

---

6.1 模擬不保證未來，但提供風險地圖

以這次模擬為例，我使用 YP-Finance 的模擬器進行 1000 次蒙地卡羅實驗，測試一個以 SPY/TLT = 70/30 比例建構的 ETF 投資組合，使用固定提領規則提領6%進行長達 30 年的退休資金提領。

結果顯示，這樣的資產配置下，提領成功率僅為 56.5%，也就是說，在 1000 次模擬中，有 435 次模擬失敗（即在 30 年內破產）。這背後傳遞出的關鍵訊息是：

即便歷史年化報酬看起來合理，若忽略波動性與提領規則之間的交互作用，仍然有將近一半的機率無法有錢享休退休人生。

這不是在否定 SPY/TLT 的組合效能，是想說明：沒有任何資產能夠保證萬無一失，只有風險分布的理解與因應

。

---

6.2 真正的高手，不是預測未來，而是設計容錯未來

再次說明這樣的模擬，不是為了尋找唯一或最佳解，是為了理解報酬的機率分布：

• 不同資產特性（如 QQQ 高波動、VT 分散、VOO 穩定）會導致什麼樣的風險曲線

• 不同提領邏輯（如固定百分比、動態調整）如何影響存續機率

• 不同退休年份起點（牛市 vs 熊市）可能導致的資產軌跡差異

投資理財無法消除不確定性，但可以透過模擬與設計，創造「與不確定性共處」的策略空間。真正的投資高手，不是準確預測未來走勢的人，而是能承受錯誤、設計出容錯結構的人。

延伸閱讀

1. Metropolis, N., & Ulam, S. (1949). The Monte Carlo Method. Journal of the American Statistical Association, 44(247), 335-341.

2. Glasserman, P. (2003). Monte Carlo Methods in Financial Engineering. Springer.

3. Boyle, P. P. (1977). Options: A Monte Carlo approach. Journal of Financial Economics, 4(3), 323-338.

4. Bodie, Z., Kane, A., & Marcus, A. (2021). Investments (12th ed.). McGraw-Hill.

5. Taleb, N. N. (2010). The Black Swan: The Impact of the Highly Improbable. Random House.

6. Sharpe, W. F. (2008). Retirement Income Scenarios: Using Monte Carlo Simulation. Financial Analysts Journal, 64(1), 18-28.

7. Vanguard Research (2021). Monte Carlo simulations: The probability of success in retirement planning. Vanguard Institutional White Paper.

8. YP-Finance 模擬器：https://tool.yp-finance.com/retirement-simulate